Solution: The way to minimize DFA using MyHill Nerode Theorem :
Step I: Divide the states of the
DFA into two subsets: fi nal (F) and non-final (Q–F).
F = {C, D, F, G}, Q–F = {A, B, E, H, I}
Make a two-dimensional matrix as shown in Fig. 3.50 labeled at the left and
bottom by the states of the DFA. Step II:1. The following combinations
are the combination of the beginning and final state.
(A, C), (A, D), (A, F), (A, G), (B, C), (B, D), (B, F), (B, G), (E, C), (E, D),
(E, F), (E, G), (H, C), (H, D), (H, F), (H, G), (I, C), (I, D), (I, F), (I, G).
Put X in these combinations of states. The modified matrix is given in

2. The pair combination of
non-final states are (A, B), (A, E), (A, H), (A, I), (B, E), (B, H), (B, I), (E,
H), (E, I), and (H, I).
r = δ(A, a) → B s = δ(B, a) → C
in the place of (B, C) there
is X. So, in the place of (A, B), there will be x.
Similarly,
(r, s) = δ((A, E), a) → (B, F) (there is X). In the place of (A, E), there will
be x.
(r, s) = δ((A, H), a) → (B, H) (neither X nor x). In the place of (A, H), there
will be 0.
(r, s) = δ((A, I), a) → (B, I) (neither X nor x]. In the place of (A, I), there
will be 0.
(r, s) = δ((B, E), a) → (C, F) (neither X nor x). In the place of (B, E), there
will be 0.
(r, s) = δ((B, H), a) → (C, H) (there is X). In the place of (B, H), there will
be x.
(r, s) = δ((B, I), a) → (C, I) (there is X). In the place of (B, I), there will
be x.
(r, s) = δ((E, H), a) → (F, H) (there is X). In the place of (E, H), there will
be x.
(r, s) = δ((E, I), a) → (F, I) (there is X). In the place of (E, I), there will
be x.
(r, s) = δ((H, I), a) → (H, I) (neither X nor x). In the place of (H, I), there
will be 0.
3. The pair combination of final
states are (C, D), (C, F), (C, G), (D, F), (D, G), and (F, G).
(r, s) = δ((C, D), a) → (H, I) (neither X nor x). In the place of (C, D), there
will be 0.
(r, s) = δ((C, F), a) → (H, H) (there is dash, neither X nor x). In the place
of (C, F), there will be 0.
(r, s) = δ((C, G), a) → (H, H) (neither X nor x). In the place of (C, G), there
will be 0.
(r, s) = δ((D, F), a) → (I, H) (neither X nor x). In the place of (D, F), there
will be 0.
(r, s) = δ((D, G), a) → (I, H) (neither X nor x). In the place of (D, G), there
will be 0.
(r, s) = δ((F, G), a) → (H, H) (neither X nor x). In the place of (F, G), there
will be 0.
The modified matrix becomes as The combination of entries 0
are the states of the modified machine. The states of the minimized machine are [A], [B, E], [C, D], [C, F], [C, G], [D, F], [D, G], [F, G], and
[H, I].
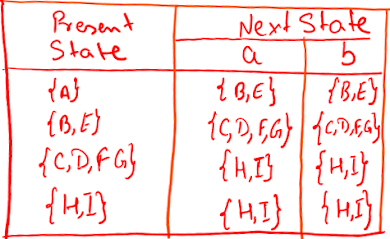
For the minimized machine M′
Q′ = ({A}, {B, E}, {C, D, F, G}, {H, I}). [C, D], [C, F], [C, G], [D, F], [D,
G], and [F, G] are combined to a new state [CDFG]. Σ = {a, b} δ′: (given in the following table)
q′0 :
{A}
F′ :
{C, D, F, G}
Also, Study about: Also Read, some interview tips |














No comments